Uniaxial analysis

The specific property of uniaxial computation methods is that they convert the complex local stress or strain state in some examined point to one scalar value, which is the only input into the damage parameter of any uniaxial criteria for fatigue damage computation. The reduced equivalent value is achieved in PragTic either via

* von Mises equivalent stress:

* Tresca’s maximum shear stress theory, where the diameter of the maximum Mohr's circle (the diffference between maximum and minimum principal stress) is looked for:

* signed von Mises equivalent stress with a sign based on the sign of the first stress invariant:

* modified equivalent stress on a plane (this option is based on the proposal introduced in FemFat v.4.6):

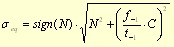where N and C are the normal and shear stress on some examined plane and the symbols f-1 and t-1 stand for fatigue limits in fully reversed push-pull and fully reversed torsion.

Note: This last definition of the equivalent stress is a junction point to multiaxial methods, since it utilizes the scheme common there. The distinction between uniaxial and multiaxial methods starts to disperse and it is probable that in some next version of PragTic this differentiation will not be used anymore.

The uniaxial methods are efficient for solution of cases where is only one load channel, or where more load channels act proportionally. If there is a non-proportional loading, the arising rotation of principal directions cannot be correctly reproduced in uniaxial methods – here the solution obtained from multiaxial methods should be preferred. The latest solution by modified equivalent stress on a plane has to be checked towards experimental data in order to estimate how much such a solution allows to introduce the multiaxial loading into the calculation.

uniaxial methods within local elastic-plastic strain methods

uniaxial methods within local elastic stress methods

This help file has been generated by the freeware version of HelpNDoc